Blackbody Calculator

Units of Wavenumbers

Yet a third spectral unit, commonly used in spectroscopy, is wavenumber, the number of waves per cm: σ = ν /100c  cm^-1.  Converting (1) to these units gives

                              .

                                                      (13)

Again, the peak is where the derivative with respect to wavenumber vanishes:

so

                                                        .                                            (14)

The peak value is

                               .                    (15)

The spectral photon radiance is found by dividing L_σ by the energy of a photon, 100hcσ :

                .      (16)

We next find the wavenumber at the peak of the spectral photon radiance:

and                                                .                                            (17)

The peak spectral photon radiance is

                     .                    (18)

Fig. 3 shows plots of L_σ and L_σ^P for various temperatures.  Note again the important difference between the spectral radiance and spectral photon radiance.

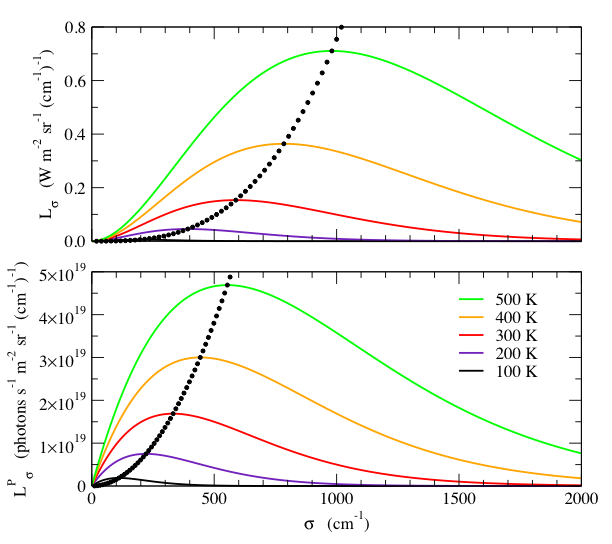
Fig. 3 - Spectral radiance, L_σ , (top) and the spectral photon radiance, L_σ^P, (bottom) as a function of wavenumber, σ, for various temperatures.  The small black dots indicate the wavenumber and value of the peak, at 10 K temperature intervals.  Note that L_σ and  L_σ^P have different wavenumber dependences.  Although the peak wavenumber is proportional to T for both quantities, L_σ peaks at a higher wavenumber than L_σ^P.  Furthermore, the peak value of L_σ increases as T ³, whereas the peak value of L_σ^P increases as T ².